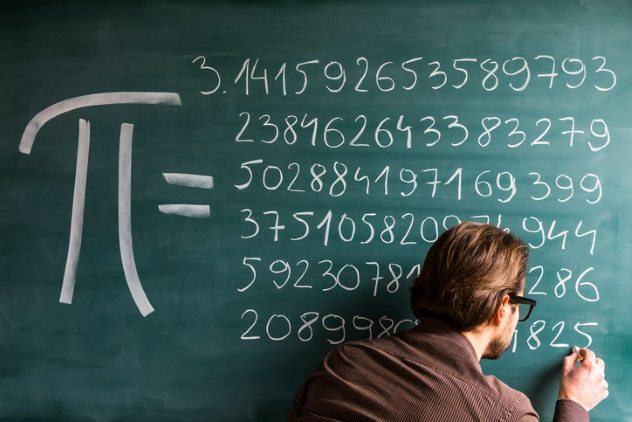First, the numeral system just about everyone reading this probably uses is called the Arabic numeral system or, more recently, the Hindu-Arabic numeral system. The original name is a misnomer, since it was invented in India and not in the Middle East.[1] However, they’re called “Arabic numerals” because Europeans thought they were invented by the Arabs. It’s not the just the numeral system that has a fascinating origin; individual numbers also have their own fascinating and downright surprising histories. Here are ten of them.
10‘Billion’
A billion, a one followed by nine zeros, is a thousand million. However, a little over four decades ago, the word “billion” referred to two different numbers. The first is a thousand million (a one and nine zeros), which remains a billion today, while the other is a million million (a one and 12 zeros), which we call a trillion today. This duality is due to differences between American and British English. American English has always recognized a billion as a thousand million, while British English used to recognize a billion as a million million. At the same time, British English recognized a thousand million (today’s billion) as a milliard. Likewise, there were two trillions. The first is the million million (a one and 12 zeros), which American English has always recognized as a trillion, while the other was a million million million (a one and 18 zeros), which British English recognized as a trillion. However, all these changed in 1974, when British English dumped the milliard and their definitions of billions and trillions for that of the Americans.[2]
9 40
How do you spell 40: “f-o-r-t-y” or “f-o-u-r-t-y?” Apparently, it’s the former. This has often confused even native English speakers, who sometimes add a “u” to “forty.” The reason for this confusion isn’t far-fetched. Most speakers assume that “forty” is derived from “four,” which has a “u.” Worse is that “fourty” hasn’t always been wrong and was once the correct spelling of 40. To explain the disparity, we first need to understand that “forty” was not derived from “four.” “Forty” was derived from Old English “feowertig,” which came from “feower,” which means “four,” and “tig,” which means “group of tens.” “Four” itself was “feower.” “Feowertig” and “feower” soon metamorphosed into “fourty” and “four.” However, this changed between the 15th and 17th centuries, during the Great Vowel Shift, which saw some words of the English language lose their vowel sounds and change in pronunciation. It was around the 16th century that “forty” first appeared. By the 1800s, “forty” appeared more frequently and soon overtook “fourty” to become the standard spelling.[3]
8 ‘Million’
The word “million” was introduced into the English language in the 14th century. The name was derived from the Old French million and Italian millione (“great thousand”), which were both derived from the Latin mille, which means “thousand.” English lacked a formal name for “million” for centuries because no one had any need for it. Apparently, no one had possessions or whatever that required them to count in millions. However, all this changed when people started counting in millions. First, they turned to the thousand, which had hitherto been the highest numerical value with an English name. “Thousand” was called “þusend,” which means “strong hundred” with “þ” being the now-extinct letter called the thorn. A million was called “þusend þusend” (thousand thousand) until million was borrowed from Old French.[4]
7 Googol
A googol is one followed by 100 zeros. Back in 1996, the search engine we know today as Google was called BackRub. In 1997, Larry Page, one of Google’s co-founders, started deliberating with some friends on what to rename the search engine. One of the friends involved in the brainstorming session was Sean Anderson, who proposed the name “Googolplex,” which refers to one followed by a googol of zeros. However, Larry opted for plain old googol. Sean checked the Internet to find out if “googol.com” had been taken. However, he erroneously spelled “googol” as “google.” Larry liked the spelling, and Google was born. What many do not realize is that “googol” and “googolplex” were coined by a nine-year-old in 1920. The child was Milton Sirotta, the nephew of mathematician Edward Kasner, who came up with the name after Kasner asked him what he could call a one followed by a 100 zeros. Sirotta suggested that only a silly name like “googol” could refer to such number. At the same time, he suggested the name “googolplex” for one followed by as many zeros as whoever was writing it out got tired. However, Kasner later defined a googolplex as one followed by a googol of zeros.[5]
6 Pi
Pi is the mathematical constant for the ratio of the circumference of a circle and its diameter. It is an infinite number but is often rounded to 3.14 or 3.142. The value of pi has puzzled and interested humans since at least 1900 BC, when ancient Babylonians calculated it to be 3.125, whereas ancient Egyptians estimated it to be 3.16. Archimedes of Syracuse is believed to be the first person to accurately calculate the value of pi. He calculated it to be a number between 3.1408 and 3.14285. In 1874, William Shanks calculated pi to 707 digits, although he was only correct until the 527th digit. In 1945, D.F. Ferguson calculated it to 620 digits, and by 1947, he had calculated it to 710 digits. In 1999, Takahashi Kanada calculated pi to 206,158,430,000 digits, and in 2011, Shigeru Kondo calculated it to ten trillion digits. One of the most hilarious incidents involving the value of pi occurred in 1897, when the Indiana state legislature almost passed a bill that would have pegged its value at 3.2. The bill wasn’t intended to change the value of pi but to solve the old-timey mathematical problem of squaring the circle. However, it would have inadvertently changed the value of pi from 3.14 to 3.2. The idea was that the area of a circle could be determined by using a ruler and compass to draw a square with the same area as the circle and then measuring it. No mathematician has ever solved this problem, but Edward Goodwin claimed to have done so in 1894. He copyrighted his solution and demanded that anyone interested in seeing it pay royalties. However, Goodwin offered it free off charge to Indiana schools on the condition that the state legislature passed a bill confirming his solution as being legitimate. This was a problem, since Goodwin used 3.2 as pi, which is wrong. The state of Indiana almost approved the bill but backed off when Professor C.A. Waldo of Purdue University informed them that they were about to unwittingly turn the value of pi to 3.2.[6]
5 Zero
Zero was first used by the Sumerians between 4,000 and 5,000 years ago. They didn’t use it as a number or to represent nothing. Instead, they added it to single numbers to denote tens and hundreds. The zero as we know it today was invented twice. The first time was in Babylon between 400 and 300 BC. However, it still wasn’t a full-fledged number but a placeholder used to represent nothing. The Maya also independently invented zero in the first few centuries of the Common Era. In the fifth century, Indian mathematician Brahmagupta became the first person to use zero as a number. He represented it with a dot, which he wrote under other numbers. By AD 879, zero was still struggling to be recognized as a number, even though it had taken the oval shape we associate with it today. However, it was usually written in a smaller font relative to other numbers. Zero only became a full-fledged number when Italian mathematician Fibonacci introduced it, along with the Arabic numerals, into Europe around 1200. Fibonacci had gained knowledge of the Arabic numerals by studying the works of Muslim scholar Mohammed ibn-Musa al-Khowarizmi, who called zero sifr. Italian traders and German bankers quickly adopted the much-needed zero, but most European governments banned Arabic numerals because they had reservations about the ease with which the numbers could be changed. However, merchants and bankers secretly continued using zero in their dealings by representing it with a code. This is the origin of the word “cipher,” which means “code.” It was derived from sifr, al-Khowarizmi’s name for zero.[7]
4 Belphegor’s Prime
Belphegor’s Prime is a one followed by 13 zeros, three sixes, and another 13 zeros before ending with a one. For a visual representation, that’s 1,000,000,000,000,066,600,000,000,000,001. The number is named after Belphegor, one of the seven princes of Hell. It is unique in many ways. Despite its length, Belphegor’s Prime is, not surprisingly, a prime number, which means it is only divisible by one and itself. At the same time, it is also a palindrome number, since it remains the same when read from either end. Then, it has 666, the famed number of the beast, right in its middle. If that’s not enough, it contains 31 numbers, which when read in reverse, gives “13,” which is considered an unlucky number. Belphegor’s Prime was discovered by Harvey Dubner, who had a fondness for uncovering new prime numbers. Dubner discovered the number after realizing other prime numbers could be derived from palindromic prime numbers like 16,661, if 13, 42, 506, 608, 2,472, and 2,623 zeros were added in between some numbers at either ends. In this case, 13 zeros were added between the ones and the sixes on each side. The number remained just another palindromic prime number until mathematician Cliff Pickover named it after a prince of Hell because it contained 666.[8]
3 5,040
5,040 might seem like just another random number to us, but not to ancient Greek philosopher Plato, who regarded it as the perfect number. 5,040 belongs to a rare group of numbers called highly composite numbers or anti-prime numbers. Unlike prime numbers, which are only divisible by one and themselves, anti-prime numbers are divisible by a lot of numbers. 5,040 is divisible by 60 numbers. Plato promoted 5,040 as the perfect number and proposed that a perfect city should not have more than 5,040 citizens. This, he thought, would allow for easy governance and division of citizens into different demographics as required.[9] To maintain this perfect number, Plato proposed that new cities should be divided into 5,040 plots and shared among 5,040 citizens. Women, children, and slaves did not count as citizens in ancient Greece, so the city’s population would have been more than 5,040. To prevent the division of a plot, whenever a citizen died, Plato suggested that an entire plot should be willed to a single preappointed son of the late citizen. The other sons were to be given to citizens who had no sons, while the daughters were to be married off. Plato also suggested that the government discourage citizens from having too many children, but when that happened, such children should be sent to another city.
2 666
Most people should be familiar with 666, which is infamous for being the number of the Biblical beast that would rule over the Earth in the last days. This is evident in Revelation 13:18, which says: “Here is wisdom. Let him that hath understanding count the number of the beast: for it is the number of a man; and his number is six hundred threescore and six.” A score is 20, and three scores is 60. So, “six hundred threescore and six” is 666. Or is it? According to a fragment of the Book of Revelation discovered in 2005, the number of the beast is 616 and not 666. The fragment is the oldest surviving record of the Book of Revelation and was written at the end of the third century. It was discovered in Egypt and was written in Greek. Reacting to the news that 616 is the number of the beast and not 666, Peter Gilmore, high priest of the Church of Satan, stated that their religious movement identified itself with 666 because of its negative connotation in Christianity. However, they would not hesitate to switch to 616 if Christians switched.[10]
1 100
The word we use for the figure above is “hundred.” However, centuries ago, the term “hundred” referred to two different numbers. The first is five scores (100), which remains today’s “hundred,” while the other was six scores (120). The disparity could be traced to Old Norse, where “hundred” was called hundrath and referred to 120. This created problems when it was introduced into English, where a “hundred” was 100. To avoid confusion, the five-score “hundred” was called the “new hundred,” “short hundred,” or “decimal hundred” (hundrath ti-raett), while the six-score “hundred” was called “old hundred,” “long hundred,” or “duodecimal hundred” (hundrath tolf-roett). However, the six-score “hundred” soon gave way to the five-score “hundred.”[11]